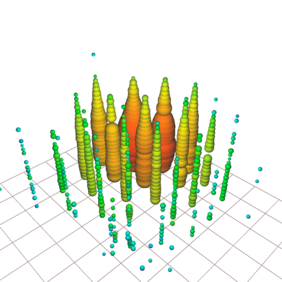
On December 6, 2016, a high-energy electron antineutrino hurtled to Earth from outer space at close to the speed of light carrying 6.3 petaelectronvolts (PeV) of energy. Deep inside the ice sheet at the South Pole, it smashed into an electron and produced a particle that quickly decayed into a shower of secondary particles. The interaction was captured by the IceCube Neutrino Observatory buried into the Antarctic Ice of the South Pole.
The measurement confirms the Standard Model
IceCube had seen a Glashow resonance event, a phenomenon predicted by Nobel laureate physicist Sheldon Glashow in 1960. With this detection, scientists provided another confirmation of the Standard Model of particle physics. Sheldon Glashow first proposed this resonance in 1960 when he was a postdoctoral researcher at what is today the Niels Bohr Institute in Copenhagen, Denmark. There, he wrote a paper in which he predicted that an antineutrino could interact with an electron to produce an as-yet undiscovered particle—if the antineutrino had just the right energy—through a process known as resonance.
Energy for Glashow resonance much higher than expected in 1960
When the proposed particle, the W– boson, was finally discovered in 1983, it turned out to be much heavier than what Glashow and his colleagues had expected back in 1960. The Glashow resonance would require a neutrino with an energy of 6.3 PeV, almost 1,000 times more energetic than what CERN’s Large Hadron Collider is capable of producing. In fact, no human-made particle accelerator on Earth, current or planned, could create a neutrino with that much energy.
But what about a natural accelerator—in space? The enormous energies of supermassive black holes at the centers of galaxies and other extreme cosmic events can generate particles with energies impossible to create on Earth. Such a phenomenon was likely responsible for the 6.3 PeV antineutrino that reached IceCube in 2016.
Only the third IceCube event with energies above 5PeV
Since IceCube started full operation in May 2011, the observatory has detected hundreds of high-energy astrophysical neutrinos and in 2018 for the first time identified a blazar as a source of cosmic neutrinos. But the Glashow resonance event is especially noteworthy because of its remarkably high energy; it is only the third event detected by IceCube with an energy greater than 5 PeV.
Neutrinos with extraterrestrial origins
“This result proves the feasibility of neutrino astronomy—and IceCube’s ability to do it—which will play an important role in future multimessenger astroparticle physics,” says Christian Haack, who was a graduate student at RWTH Aachen while working on this analysis and is now a postdoctoral researcher in the group of Prof. Elisa Resconi at Technical University of Munich. “We now can detect individual neutrino events that are unmistakably of extraterrestrial origin.”
First measurement of antineutrino in astrophysical neutrino flux
The result also opens up a new chapter of neutrino astronomy because it starts to disentangle neutrinos from antineutrinos. Previous measurements have not been sensitive to the difference between neutrinos and antineutrinos, so this result is the first direct measurement of an antineutrino component of the astrophysical neutrino flux.
There are a number of properties of the astrophysical neutrinos’ sources that cannot be measured, like the physical size of the accelerator and the magnetic field strength in the acceleration region. But through determining the neutrino-to-antineutrino ratio, these properties can be indirectly investigated.
To confirm the detection and make a decisive measurement of the neutrino-to-antineutrino ratio, the IceCube Collaboration wants to see more Glashow resonances. A proposed expansion of the IceCube detector, IceCube-Gen2, would enable the scientists to make such measurements in a statistically significant way. The collaboration recently announced an upgrade of the detector that will be implemented over the next few years, the first step toward IceCube-Gen2.
More Glashow resonance events necessary
Glashow, now an emeritus professor of physics at Boston University, echoes the need for more detections of Glashow resonance events. “To be absolutely sure, we should see another such event at the very same energy as the one that was seen,” he says. “So far there’s one, and someday there will be more.”
The IceCube Neutrino Observatory is funded primarily by the National Science Foundation and is headquartered at the Wisconsin IceCube Particle Astrophysics Center, a research center of UW–Madison, USA. IceCube’s research efforts, including critical contributions to the detector operation, are funded by agencies in Australia, Belgium, Canada, Denmark, Germany, Japan, New Zealand, Republic of Korea, Sweden, Switzerland, the United Kingdom, and the United States. IceCube construction was also funded with significant contributions from Belgium, Germany, Sweden as well as from the University of Wisconsin–Madison, USA.
Original Publication
R. Abbasi et al. (The IceCube Collaboration): ‘Detection of a particle shower at the Glashow resonance with IceCube’, Nature, 11 March 2021
DOI: 10.1038/s41586-021-03256-1
Contact
Technical University of Munich
Dr. Christian Haack
Physics Department
Professorship for experimental physics with cosmic particles/Chair Prof. Resconi
James-Franck-Str. 1, D-85748 Garching, Germany
E-Mail: christian.haack@tum.de